之前在研究矩阵乘积态的时候,遇到了大量繁琐的矩阵(其实是张量)点积,看得头晕脑胀不得要领。The density-matrix renormalization group in the age of matrix product states介绍了一种用图像(diagram)表示这种点积的方法,初看好似鬼画符,看懂之后却显得非常简洁明了。如下图,即表示了一个六阶张量。
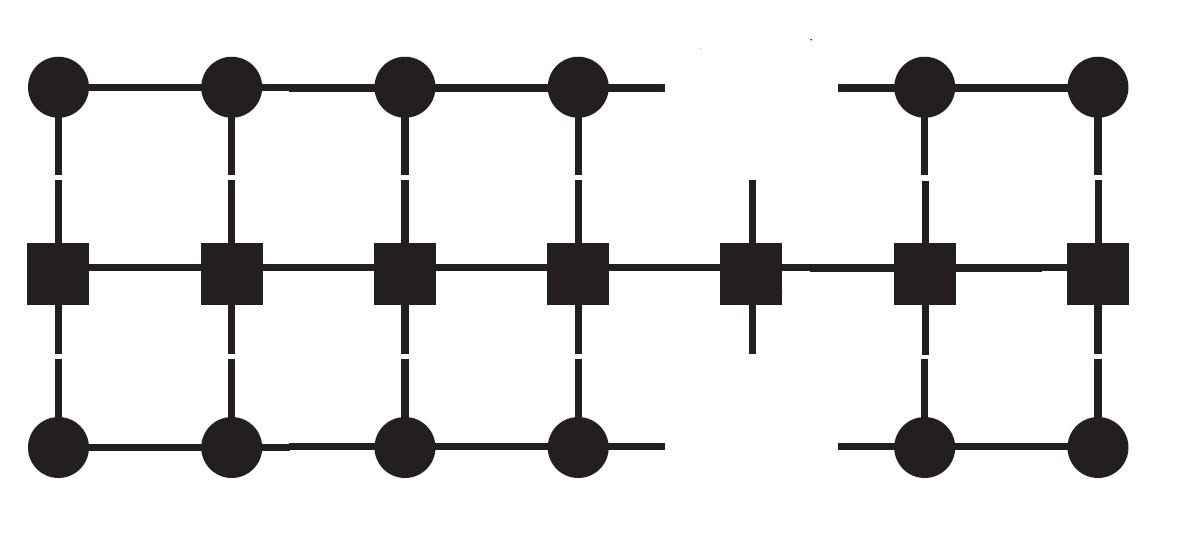
我自认线性代数学的还凑合,但掌握这种方法之后对矩阵特别是张量的理解瞬间提升了一个档次。另外,上网搜索没有发现任何有关的资料(2018年9月26日又及:有眼不识泰山,这里有一个非常好的tutorial)。
众所周知,图像就是矩阵(张量),为了不引起混淆,这里明确说明“矩阵(张量)点积的图形化表达”与计算机视觉没有半毛钱关系。如果硬要说关系,那就是两者都和矩阵有关。
这里还要说明,线性代数是有几何背景的,矩阵也可以理解为某种算符,所以在一个二维坐标系下,可以将一个二阶矩阵的作用画出来,帮助理解矩阵的意义和作用。本文中“矩阵(张量)点积的图形化表达”和这也没有半毛钱关系,除了两者都和矩阵有关以外。
Penrose graphical notation倒是和本文中“矩阵(张量)点积的图形化表达”有点类似,不过前者过于繁复,非数学专业恐怕用起来有点费劲。
以下为了编辑方便,用字符来画图。 看起来有点费眼睛,但精确度很高,绘制、修改比较省事省力。
首先,很简单,我们把一个矩阵画成一个方块(你可以想象它是■或者□,但为了排版好看用#表示),非常直观吧?1
把它记为\(A\)。我们假设\(A\)的大小是\(m\times n\),进一步记为\(A_{m\times n}\)。为了表示这些信息,可以让这个表示\(A_{m\times n}\)的小方块伸出来两个脚,分别写上\(m\)和\(n\)。1
2 m n
---#---
下面假设有矩阵\(B_{n\times l}\),不难仿照\(A_{m\times n}\)画出\(B_{n\times l}\):1
2
3 n l
---#---
B
为了清晰起见,我在#下方标注了\(B_{n\times l}\)。熟悉矩阵的同学想必早已忍不住要做矩阵点积了:\(A_{m\times n}B_{n\times l} = C_{m\times l}\)。那么,怎样表示\(A_{m\times n}B_{n\times l}\)呢?很简单:1
2
3 m n l
---#---#---
A B
把它们维数为\(n\)的脚连起来就好了~
注意到,连起来之后的图形也伸出来两个脚,它表示的矩阵大小为\(m\times l\)。也就是说,上面那个“图”表示了\(C_{m\times l}\)。矩阵点积把总维数为4的两个量变成了一个总维数为2的量,我觉得这才是张量收缩(contraction)这一词的来源。
如果用计算机语言来表示\(A_{m\times n}B_{n\times l}\):1
2
3
4
5
6
7
8
9// C已经被初始化为一个初值都为0的M*L数组
// 以下写法不是速度最快的,但可能是最清晰的
for (int m = 0; m < M; m++){
for (int l = 0; l < L; l++){
for (int n = 0; n < N; n++){
C[m][l] += A[m][n] * B[n][l];
}
}
}
我们可以看出,\(A_{m\times n}B_{n\times l}\)其实就是\(A_{m\times n}\)和\(B_{n\times l}\)消去它们共同的指标(index)n的过程,信息被压缩,存储在C中。所以,用两个方块的脚连在一起表示矩阵点积,体现了contraction的特性和矩阵点积的本质。
吹了半天牛逼,好像没什么卵用?接下来是这种图形化表达的一些应用。
张量
张量是什么-逼乎?我在刚学张量的时候也是一头雾水。知乎大神一通操作,对我来说并没有什么有效信息,竟然也骗了2k个赞。现在张量也是很火的,说一句tensor,立马就显得很有逼格,好像很懂tensorflow,非常熟悉矩阵的各种理论一样。其实对于搞计算机的来说,张量说白了就是高维数组。只不过高维数组这个数据结构定义很直观,但要操作起来很头疼。因为张量的一大作用就是做点积,而给两个高维数组定义点积这么一个操作让人有点摸不着头脑。
不过有图有好说了。
比如张量\(A_{i\times j \times k}\)有三个指标,可以伸出来三个脚,表示为:1
2
3
4 j
i | k
---#---
A
而\(B_{k\times l \times m \times n}\)可以表示为:1
2
3
4
5
6 m
k | l
---
|
n
B
如果没有图形的基础,对这两个矩阵做contraction显得非常抽象。而一旦我们理解了contraction就是把矩阵的两条腿连起来,做contraction就变得很直观。首先我们立刻就明白了为什么做contraction要说明是对哪个指标做contraction,因为这决定了我们要连哪两条腿。现在假设对这两个矩阵维度为\(k\)的指标做contraction,我们得到:1
2
3
4
5
6 j m
i | k | l
---
|
n
A B
得到的结果张量大小为\(i\times j \times l \times m \times n\),相应的计算代码为:1
2
3
4
5
6
7
8
9
10
11
12
13
14// C已经被初始化为一个初值都为0的I*J*L*M*N数组
for (int i = 0; i < I; i++){
for (int j = 0; j < J; j++){
for (int l = 0; l < L; l++){
for (int m = 0; m < M; m++){
for (int n = 0; n < N; n++){
for (int k = 0; k < K; k++){
C[i][j][l][m][n] += A[i][j][k] * B[k][l][m][n];
}
}
}
}
}
}
这代码本来可以当做“糟糕代码”的典型,但如果用图形的方式来理解,高维数组点积的定义立刻就变得很清楚,如果把我上面画的图当做文档加进去,我想就不会有人再抱怨。numpy的tensordot函数“声明”为np.tensordot(a, b, axes=2),其意义在图形方式下也变得直观明朗。
至此,本文最开始给出的“六阶张量”图也很容易理解了。图中出现的方块和圆形记号没有本质区别,都是张量的表示,只不过在那张图的语境下,方块张量和圆形张量物理上有不同含义而已。
矩阵(张量)转置
矩阵的转置很平凡:1
2
3 m n n m
---#--- --transpose--> ---#---
A A
但张量的转置似乎就不太好定义了。不难想象,张量的转置需要明确定义转置后各个指标的位置。看看np.transpose的文档吧。
下面我们来“证明”一个经典公式\((AB)^T=B^TA^T\),考虑\(A_{m\times n}\)和\(B_{n\times l}\)。1
2
3 m n l l n m
(---#---#---)^T == ---#---#---
A B B^T A^T
这才是数学证明中的“显然”。这种图形化的表示方法本质上是按照定义进行的乘法和加法操作,进行这种证明时绕开了繁琐的\(\Sigma\)符号,也就无往而不利。
矩阵点积的性质
我们考虑两个矩阵点积的性质,其一是结合律,即\(A(BC)=(AB)C\)。这个很显然。
其二是交换律。对于不是方阵的情况,盲目交换的问题是显然的(segmentation fault!):1
2
3 m n l n l m n
---#---#--- != ---#--- ?? ---#---
A B B A
假设\(m=l\),那么上面所绘制的操作就有定义了,但不难看出\(AB\)和\(BA\)进行的完全是两种运算,一般地\(AB \neq BA\)。
矩阵的迹(trace)
学线代的时候对矩阵的迹感觉非常奇怪,好好一个矩阵,只从中抽取对角元,能有什么信息?还有这么多性质?即使告诉你迹是一个矩阵对自己做contraction,也是懵懵懂懂。下面我们来看\(A_{n\times n}\)的迹:1
2
3
4
5 n n
---#---
| |
-------
A
这一表示已经包含了一定信息,比如迹的结果是一个数,比如迹只对方阵有定义,比如求迹的代码:1
2
3
4double trace = 0;
for (int i = 0; i < n; i++){
trace += A[i][i];
}
和之前的两个代码颇为神似。我们也可以“证明”一些迹的简单的性质,比如\(\textrm{tr}(AB)=\textrm{tr}(BA)\):1
2
3
4---#---#--- ---#---#---
| | == | |
----------- -----------
A B B A
像\(\textrm{tr}A^T=\textrm{tr}A\)之类一眼就能看出。
还有“偏迹(partial trace)”的概念。如果你去看wikipedia,包你看个痛。不过如果我们这么看一个四阶张量的偏迹:1
2
3
4 |
---#---
| |
----
就非常的简单直观。
最后,让我们再“证明”一个量子力学中的定理吧。对于由\(\left | \psi_j \right >\)为纯态形成的混合态,其密度矩阵定义为:
$$
\rho = \Sigma_j p_j \left | \psi_j \right > \left < \psi_j \right |
$$其中\(p_j\)为相应纯态的出现概率。定义这样一个密度矩阵的好处有很多,比如对于一个物理量\(A\),其期望值\(\left < A \right > \)可以这么求:
$$
\left < A \right > = \textrm{tr} (\rho A)
$$左边按照定义展开是\(\Sigma_j p_j \left < \phi_j \right | A \left | \phi_j \right >\),右边展开后调换一下求和顺序得到\(\Sigma_j p_j \textrm{tr} \left (\left | \phi_j \right > \left < \phi_j \right | A \right )\)。不难发现,证明的关键在于:
$$
\left < \phi_j \right | A \left | \phi_j \right > = \textrm{tr} \left (\left | \phi_j \right > \left < \phi_j \right | A \right )
$$为了方便不那么熟悉量子力学这一套黑话的朋友,也方便我接下来“画图”,我们用数学语言把这个要证明的式子再写一遍:
$$A_{1\times n}B_{n\times n}C_{n\times 1}=\textrm{tr}(C_{n\times 1}A_{1\times n}B_{n\times n})
$$接下来就是见证奇迹的时刻。
首先,等号左边:1
2
3 1 n n 1
---#-----#-----#---
A B C
注意到,这个表示结果是一个数(\(1\times 1\)的矩阵),而一个数的迹还是它自己,即:1
2
3
4
5 1 n n 1 1 n n 1
---#-----#-----#--- == ---#-----#-----#---
A B C | |
-------------------
A B C
我们把这个环做一下旋转,把C从右边移到左边,因为我们没有改变任何一个contraction,式子的值保持不变:1
2
3
4
5 1 n n 1 n 1 n n
---#-----#-----#--- ---#-----#-----#---
| | == | |
------------------- -------------------
A B C C A B
式子的右边即是\(\textrm{tr}(C_{n\times 1}A_{1\times n}B_{n\times n})\)。
局限性
这种表示矩阵的图形方法对理解复杂的矩阵运算是非常有效的,但是存在一个很致命的问题,就是对矩阵加法这一操作没有什么表现力。